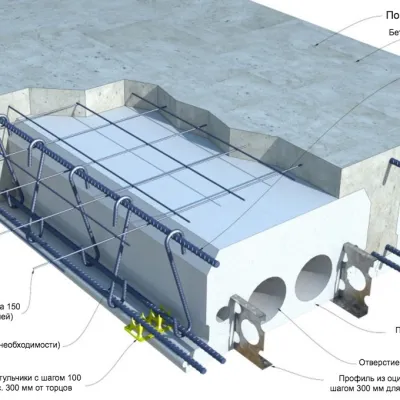
Несмотря на то что заводы железобетонных изделий производят большое количество готовой продукции, все же иногда приходится делать железобетонную балку перекрытия или железобетонную перемычку самому. А при строительстве дома с использованием несъемной опалубки без этого просто не обойтись.
Практически все видели строителей-монтажников, засовывающих в опалубку какие-то железяки, и почти все знают, что это - арматура, обеспечивающая прочность конструкции, вот только определять количество и диаметр арматуры или сечение горячекатаных профилей, закладываемых в железобетонные конструкции в качестве арматуры, хорошо умеют только инженеры-технологи. Железобетонные конструкции, хотя и применяются вот уже больше сотни лет, но по-прежнему остаются загадкой для большинства людей, точнее, не сами конструкции, а расчет железобетонных конструкций. Попробуем приподнять завесу таинственности над этой темой примером расчета железобетонной балки.
Расчет любой строительной конструкции вообще и железобетонной балки в частности состоит из нескольких этапов. Сначала определяются геометрические размеры балки.
Этап 1. Определение длины балки.
Рассчитать реальную длину балки проще всего. Главное, что мы заранее знаем пролет, который должна перекрыть балка, а это уже большое дело. Пролет - это расстояние между несущими стенами для балки перекрытия или ширина проема в стене для перемычки. Пролет - это расчетная длина балки, реальная длина балки будет конечно же больше. Так как балка висеть в воздухе не может (я думаю над этим, но пока решение не найдено), значит, длина балки должна быть больше пролета на ширину опирания на стены. И хотя все дальнейшие расчеты производятся по расчетной, а не по реальной длине балки, определить реальную длину балки все-таки нужно. Ширина опор зависит от прочности материала конструкции под балкой и от длины балки, чем прочнее материал конструкции под балкой и чем меньше пролет, тем меньше может быть ширина опоры. Теоретически рассчитать ширину опоры, зная материал конструкции под опорой можно точно также, как и саму балку, но обычно никто этого не делает, если есть возможность опереть балку на кирпичные, каменные и бетонные (железобетонные) стены на 150-300 мм при пролетах 2-10 метров. Для стен из пустотелого кирпича и шлакоблока может потребоваться расчет ширины опоры.
Для примера примем значение расчетной длины балки = 4 м.
Этап 2. Предварительное определение ширины и высоты балки и класса (марки) бетона.
Эти параметры нам точно не известны, но их следует задать, чтобы было, что считать.
Если это будет перемычка, то логично из конструктивных соображений сделать перемычку шириной, приблизительно равной ширине стены. Для балок перекрытия ширина может быть какой угодно, но обычно принимается не менее 10 см и кратной 5 см (для простоты расчетов). Высота балки принимается из конструктивных или эстетических соображений. Например, для кирпичной кладки логично сделать перемычку высотой в 1 или 2 высоты кирпича, для поризованного блока - в 1 высоту блока и так далее. Если балки перекрытия будут видны после окончания строительства, то также логично сделать высоту балки пропорциональной ширине и длине балки, а также расстоянию между балками. Если балки перекрытия будут бетонироваться одновременно с плитой перекрытия, то полная высота балки при расчетах будет составлять: видимая высота балки + высота монолитной плиты перекрытия.
Для примера примем значения ширины = 10 см, высоты = 20 см, класс бетона В25.
Этап 3. Определение опор.
С точки зрения сопромата, будет ли это перемычка над дверным или оконным проемом или балка перекрытия, значения не имеет. А вот то как именно балка будет опираться на стены имеет большое значение. С точки зрения строительной физики любую реальную опору можно рассматривать или как шарнирную опору, вокруг которой балка может условно свободно вращаться или как жесткую опору. Другими словами жесткая опора называется защемлением на концах балки. Почему столько внимания уделяется опорам балки, станет понятно чуть ниже.
1. Балка на двух шарнирных опорах.
Если железобетонная балка устанавливается в проектное положение после изготовления, ширина опирания балки на стены меньше 200 мм, при этом соотношение длины балки к ширине опирания больше 15/1 и в конструкции балки не предусмотрены закладные детали для жесткого соединения с другими элементами конструкции, то такая железобетонная балка однозначно должна рассматриваться как балка на шарнирных опорах. Для такой балки принято следующее условное обозначение:

2. Балка с жестким защемлением на концах.
Если железобетонная балка изготавливается непосредственно в месте установки, то такую балку можно рассматривать, как защемленную на концах только в том случае, если и балка и стены, на которые балка опирается, бетонируются одновременно или при бетонировании балки предусмотрены закладные детали для жесткого соединения с другими элементами конструкции. Во всех остальных случаях балка рассматривается, как лежащая на двух шарнирных опорах. Для такой балки принято следующее условное обозначение:

3. Многопролетная балка.
Иногда возникает необходимость рассчитать железобетонную балку перекрытия, которая будет перекрывать сразу две или даже три комнаты, монолитное железобетонное перекрытие по нескольким балкам перекрытия или перемычку над несколькими смежными проемами в стене. В таких случаях балка рассматривается как многопролетная, если опоры шарнирные. При жестких опорах количество пролетов значения не имеет, так как опоры жесткие, то каждая часть балки может рассматриваться и рассчитываться как отдельная балка.
4. Консольная балка.
Балка, один или два конца которой не имеют опор, а опоры находятся на некотором расстоянии от концов балки, называется консольной. Например плиту перекрытия над фундаментом, выступающую за пределы фундамента на несколько сантиметров, можно рассматривать как консольную балку, кроме того перемычку, опорные участки которой больше l/5 также можно рассматривать как консольную и так далее.
Этап 4. Определение нагрузки на балку.
Нагрузки на балку могут быть самыми разнообразными. С точки зрения строительной физики все, что неподвижно лежит на балке, прибито, приклеено или подвешено на балку - это статическая нагрузка. Все что ходит, ползает, бегает, ездит и даже падает на балку - это все динамические нагрузки. Нагрузка может быть сосредоточенной, например, человека, стоящего на балке, или колеса автомобиля, опирающиеся на балку длиной 3 и более метров, можно условно рассматривать как сосредоточенную нагрузку. Сосредоточенная нагрузка измеряется в Ньютонах (по старому, в килограмм-силах (кгс)).
А вот кирпич, керамоблок или любой другой материал лежащий на перемычке, а также плиты перекрытия, снег, дождь и даже ветер, землетрясение, цунами и много чего еще можно рассматривать как распределенные нагрузки, действующие на перемычку или балку перекрытия. Кроме того распределенная нагрузка может быть равномерно распределенной, равномерно и неравномерно изменяющейся по длине и т.д. Распределенная нагрузка измеряется в Н(кгс/м2), но при расчетах используется значение распределенной нагрузки на погонный метр, так как при построении эпюр изгибающих моментов ни высота ни ширина балки не принимаются во внимание, а принимается во внимание только длина балки. Перевести квадратные метры в погонные не сложно. Если рассчитывается балка перекрытия, то распределенная нагрузка вполне логично умножается на расстояние между осями балок перекрытия. Если определяется нагрузка на перемычку, то можно плотность материала конструкции, лежащей на перемычке, умножить на ширину и на высоту конструкции.
Чем более точно мы посчитаем нагрузки, действующие на балку, тем более точным будет наш расчет и тем надежнее будет конструкция. И если со статическими нагрузками все более-менее просто, то динамические нагрузки потому и динамические что не стоят на месте и пытаются усложнить нам и без того не простой расчет.
С одной стороны конструкцию следует рассчитывать на максимально неблагоприятное сочетание нагрузок, с другой стороны теория вероятности говорит о том, что вероятность такого сочетания нагрузок крайне мала и рассчитывать конструкцию на максимально неблагоприятное сочетание нагрузок, значит неэффективно тратить строительные материалы и людские ресурсы.
Дом, построенный по всем правилам и способный выдержать практически все, включая ядерный удар, никто кроме свихнувшегося миллионера не купит, слишком дорого. Поэтому при расчете конструкций динамические нагрузки используются с различными поправочными коэффициентами, учитывающими вероятность сочетания нагрузок, но как показывает практика, учесть все невозможно. Здания, разрушающиеся во время землетрясений, ураганов, цунами и даже обильных снегопадов - яркое тому подтверждение. Чтобы хоть как-то облегчить жизнь не только инженерам-конструкторам, но и простым людям, принято рассчитывать междуэтажные перекрытия на распределенную нагрузку 400 кг/м2 (без учета веса конструкции перекрытия). Данная распределенная нагрузка учитывает практически все возможные сочетания нагрузок на перекрытия в жилых домах, тем не менее никто не запрещает рассчитывать конструкции на бoльшие нагрузки, например если на железобетонные балки будет укладываться какое-то очень тяжелое перекрытие, например железобетонные пустотные плиты добавят еще 300-330 кг/м2, мы же остановимся на значении 400 кг/м2. Конечно, можно было бы просто сказать, что мы будем рассчитывать балку на распределенную нагрузку 400 кг/м.п при шаге между балками 1 метр, но хотелось бы, чтобы Вы имели хотя бы приблизительное представление, откуда взялась эта цифра.
Этап 5. Определение максимального изгибающего момента, действующего на поперечное сечение балки.
Тут все зависит от того, какие на балку действуют нагрузки, какие у балки опоры и сколько пролетов, некоторые типы балок, рассмотренные на этапе 2, являются статически неопределимыми, и хотя все можно рассчитать самому, но не будем углубляться в теорию, проще воспользоваться готовыми формулами для наиболее характерных случаев.
Пример расчета железобетонной балки на шарнирных опорах, на которую действует распределенная нагрузка.
Максимальный изгибающий момент для балки лежащей на двух шарнирных опорах, а в нашем случае балки перекрытия, опирающейся на стены, на которую действует распределенная нагрузка, будет посредине балки:
Для пролета 4 м Мmax = (400 · 42) / 8 = 800 кг·м
Этап 6. Расчетные предпосылки:
Расчет по прочности элементов железобетонных конструкций производится для нормальных и наклонных к продольной оси сечений в наиболее напряженных местах (для этого мы и определяли значение момента).
Железобетон - это композитный материал, прочностные свойства которого зависят от множества факторов, которые точно учесть при расчете достаточно сложно. Кроме того. бетон хорошо работает на сжатие из-за относительно высоких прочностных характеристик по сжатию, а арматура хорошо работает на растяжение, а при сжатии возможно выпучивание арматуры. Поэтому конструирование железобетонной конструкции сводится к определению сжатых и растянутых зон.
В растянутых зонах устанавливается арматура. При этом высота сжатой и растянутой зоны заранее неизвестна и потому применять обычные методы подбора сечения, как для деревянной или металлической балки, не получится.
На основе накопленного опыта по расчету и работе железобетонных конструкций разработано несколько методик расчета. Далее приводится одна их них, основанная на следующих расчетных предпосылках:
- сопротивление бетона растяжению принимается равным нулю;
- сопротивление бетона сжатию принимается равномерно распределенным, равным Rпр (Rb по новому СП);
- максимальные растягивающие напряжения в арматуре равны расчетному сопротивлению растяжению Rа (Rs по новому СП);
- сжимающие напряжения в напрягаемой и ненапрягаемой арматуре принимаются не более расчетного сопротивления сжатию Rа (Rsc по новому СНиПу);
- рекомендуется применять элементы таких поперечных сечений, чтобы вычисленная по расчету относительная высота сжатой зоны бетона ξ=x/h0 не превышала ее граничного значения ξR, при котором предельное состояние элемента наступает, когда напряжения в растянутой зоне достигают расчетного сопротивления Rа.
Граничное условие имеет вид
Величина ξR определяется по формуле:
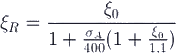
где
ξo - характеристика сжатой зоны бетона, определяемая для тяжелого бетона и бетона на пористых заполнителях по формуле:
в которой Rпр принимается в МПа; коэффициент а = 0,85 для тяжелого бетона и а = 0,8 для бетона на пористых заполнителях.
Значение напряжения σА в арматуре принимается при 0,002ЕА = 400 МПа равным для арматуры классов:
A-I, A-II, A-III, B-I и Вр-1: (Ra - σo);
A-IV, Ат-IV, A-V, At-V, At-VI, B-II, Bp-II и K-7: (Ra + 400 - σ0),
где
Ra - расчетное сопротивление арматуры растяжению с учетом коэффициентов условий работы арматуры ma, σo - значение предварительного напряжения арматуры с учетом потерь при коэффициенте точности натяжения mт < 1.
Если при расчете изгибаемых элементов учитывается коэффициент условий работы бетона mб1 = 0,85, то в формулу (6.2) вместо значения 400 подставляется 500.
Дальнейший расчет мы будем производить для балки с обычной (не преднапряженной) арматурой, при этом рассчитывать сечение арматуры мы будем только для нижней части балки, в которой действуют растягивающие напряжения, это вовсе не означает, что в верхней части балки арматуры (устанавливаемой по технологическим соображениям) не будет, но позволит значительно упростить расчет.
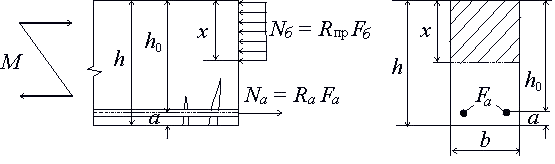
При расчете элементов прямоугольного сечения с одиночной не преднапряжённой арматурой (когда расчетная арматура устанавливается только в области растяжения) можно пользоваться вспомогательной таблицей 1 и формулами:
где
Аo =x/ho(1 - x/2ho) = ξ(1 -0,5ξ) (6.6)
η = (1 - x/2ho) = 1 - 0,5ξ (6.7)
Коэффициент армирования μ и процент армирования μ·100 (%) определяется по формулам:
μ = Fa/bho, или μ = ξRпр/Ra (6.8)
Основываясь на опыте проектирования оптимальных по стоимости железобетонных изделий рекомендуется принимать:
μ% = 1÷2%, ; ξ = 0,3÷0,4 - для балок (6.10)
μ% = 0,3÷0,6%, ξ = 0,1÷0,15 - для плит перекрытия (6.11)
Таблица 1. Данные для расчета изгибаемых элементов прямоугольного сечения, армированных одиночной арматурой (согласно "Пособия по проектированию бетонных и железобетонных конструкций из тяжелых и легких бетонов без предварительного напряжения арматуры (к СНиП 2.03.01-84)")
| ξ = x/h0 | r0=1/sqrt(A0) | η = zσ/h0 | A0 | ξ = x/h0 | r0=1/sqrt(A0) | η = zσ/h0 | A0 |
| 0,01 | 10 | 0,995 | 0,01 | 0,36 | 1,84 | 0,820 | 0,295 |
| 0,02 | 7,12 | 0,990 | 0,02 | 0,37 | 1,82 | 0,815 | 0,301 |
| 0,03 | 5,82 | 0,985 | 0,03 | 0,38 | 1,8 | 0,810 | 0,309 |
| 0,04 | 5,05 | 0,980 | 0,039 | 0,39 | 1,78 | 0,805 | 0,314 |
| 0,05 | 4,53 | 0,975 | 0,048 | 0,40 | 1,77 | 0,80 | 0,320 |
| 0,06 | 4,15 | 0,970 | 0,058 | 0,41 | 1,75 | 0,795 | 0,326 |
| 0,07 | 3,85 | 0,965 | 0,067 | 0,42 | 1,74 | 0,790 | 0,332 |
| 0,08 | 3,61 | 0,960 | 0,077 | 0,43 | 1,72 | 0,785 | 0,337 |
| 0,09 | 3,41 | 0,955 | 0,085 | 0,44 | 1,71 | 0,780 | 0,343 |
| 0,1 | 3,24 | 0,950 | 0,095 | 0,45 | 1,69 | 0,775 | 0,349 |
| 0,11 | 3,11 | 0,945 | 0,104 | 0,46 | 1,68 | 0,770 | 0,354 |
| 0,12 | 2,98 | 0,940 | 0,113 | 0,47 | 1,67 | 0,765 | 0,359 |
| 0,13 | 2,88 | 0,935 | 0,121 | 0,48 | 1,66 | 0,760 | 0,365 |
| 0,14 | 2,77 | 0,930 | 0,13 | 0,49 | 1,64 | 0,755 | 0,370 |
| 0,15 | 2,68 | 0,925 | 0,139 | 0,50 | 1,63 | 0,750 | 0,375 |
| 0,16 | 2,61 | 0,920 | 0,147 | 0,51 | 1,62 | 0,745 | 0,380 |
| 0,17 | 2,53 | 0,915 | 0,155 | 0,52 | 1,61 | 0,740 | 0,385 |
| 0,18 | 2,47 | 0,910 | 0,164 | 0,53 | 1,60 | 0,735 | 0,390 |
| 0,19 | 2,41 | 0,905 | 0,172 | 0,54 | 1,59 | 0,730 | 0,394 |
| 0,2 | 2,36 | 0,900 | 0,18 | 0,55 | 1,58 | 0,725 | 0,399 |
| 0,21 | 2,31 | 0,895 | 0,188 | 0,56 | 1,57 | 0,720 | 0,403 |
| 0,22 | 2,26 | 0,890 | 0,196 | 0,57 | 1,56 | 0,715 | 0,408 |
| 0,23 | 2,22 | 0,885 | 0,203 | 0,58 | 1,55 | 0,710 | 0,412 |
| 0,24 | 2,18 | 0,880 | 0,211 | 0,59 | 1,54 | 0,705 | 0,416 |
| 0,25 | 2,14 | 0,875 | 0,219 | 0,60 | 1,535 | 0,7 | 0,420 |
| 0,26 | 2,1 | 0,870 | 0,226 | 0,61 | 1,53 | 0,695 | 0,424 |
| 0,27 | 2,07 | 0,865 | 0,236 | 0,62 | 1,525 | 0,690 | 0,428 |
| 0,28 | 2,04 | 0,860 | 0,241 | 0,63 | 1,52 | 0,685 | 0,432 |
| 0,29 | 2,01 | 0,855 | 0,248 | 0,64 | 1,515 | 0,680 | 0,435 |
| 0,30 | 1,98 | 0,850 | 0,255 | 0,65 | 1,51 | 0,675 | 0,439 |
| 0,31 | 1,95 | 0,845 | 0,262 | 0,66 | 1,5 | 0,670 | 0,442 |
| 0,32 | 1,93 | 0,840 | 0,269 | 0,67 | 1,495 | 0,665 | 0,446 |
| 0,33 | 1,9 | 0,835 | 0,275 | 0,68 | 1,49 | 0,660 | 0,449 |
| 0,34 | 1,88 | 0,830 | 0,282 | 0,69 | 1,485 | 0,655 | 0,452 |
| 0,35 | 1,86 | 0,825 | 0,289 | 0,70 | 1,48 | 0,650 | 0,455 |
Этап 7. Расчет сечения арматуры.
Размеры поперечного сечения железобетонной балки и положение арматуры мы можем задавать сами, исходя из технологических требований или других соображений. Например, мы решили, что балка будет иметь высоту h = 20 см и ширину b = 10 см. Расстояние а центра поперечного сечения арматуры от низа балки обычно принимается в пределах 2-3 см.
Дальнейший расчет мы будем производить при а = 2 см. Расчетное сопротивление растяжению для арматуры класса А-III согласно таблице 5.8 (СП 52-101-2003 Бетонные и железобетонные конструкции без предварительного напряжения арматуры):
| Арматура классов | Расчетные значения сопротивления арматуры для предельных состояний первой группы, МПа | ||
| растяжению | сжатию Rsc | ||
| продольной Rs
| поперечной Rsw (хомутов и отогнутых стержней) | ||
| А240 | 215 | 170 | 215 |
| A300 | 270 | 215 | 270 |
| А400 | 355 | 285 | 355 |
| А500 | 435 | 300 | 435 (400) |
| В500 | 415 | 300 | 415 (360) |
| Примечание - Значения в скобках используют только при расчете на кратковременное действие нагрузки. | |||
Ra = 3600 кгс/см2 (355 МПа). Сейчас принято использовать новые обозначения для классов арматуры. Расчетное сопротивление сжатию для бетона класса В25 согласно таблице 4 Rпр (Rb) = 148 кгс/см2 (14,5 МПа, впрочем для расчетов можно использовать и приближенное значение 145 кгс/см2, это даст небольшой запас по прочности около 2%, зато не требует точного перевода МПа в кгс/см2). Теперь у нас есть все данные для определения коэффициента Аo. Преобразовав формулу (6.4) мы получим:
Аo = M/bh2oRпр = 800/(0,1·0,182·1480000) = 0,1668
Теперь по вспомогательной таблице 1 мы можем найти η = 0,907 и ξ = 0,187. Полученное значение ξ меньше рекомендуемого для балок (согласно формулы 6.10). Чтобы уменьшить стоимость балки мы можем уменьшить и ширину и высоту балки так, чтобы полученное значение ξ было в рекомендуемых пределах или уменьшить класс бетона. Для начала уменьшим высоту балки с 20 до 15 см. Тогда:
Аo = M/bh2oRпр = 800/(0,1·0,132·1480000) = 0,3264
по таблице 1 η = 0,795 и ξ = 0,41
Тогда согласно формуле (6.5) требуемая площадь сечения арматуры:
Fa = M/ηhoRa = 800/(0,795·0,13·36000000) = 0,0002152 м2 или 2,152 см2.
Таким образом для армирования нашей балки достаточно 2 стержней диаметром 12 мм. Площадь сечения арматуры составит 2,26 см2. Подбор арматуры удобно производить по таблице 2 (см. ниже).
Коэффициент армирования нашей балки согласно формулам (6.8) и (6.9) составит:
μ% = 100·0.41·148/3600 = 1,65 %
Такой процент находится в рекомендуемых пределах. Осталось проверить соблюдение граничных условий согласно формул (6.1-6.3):
ξo = 0,85 - 0,008·14,5 = 0,734
ξR = 0,734/(1 + 365/400(1 + 0,734/1,1)) = 0,2911
Граничное условие нами не соблюдено, поэтому нужно увеличить высоту балки, чтобы уменьшить относительную высоту сжатой зоны бетона. При h = 17,5 см:
Аo = M/bh2oRпр = 800/(0,1·0,1552·1450000) = 0,23
по таблице 1 η = 0,867 и ξ = 0,266
Тогда согласно формуле (6.5) требуемая площадь сечения арматуры:
Fa = M/ηhoRa = 800/(0,867·0,155·36000000) = 0,0001653 м2 или 1,653 см2.
для армирования нашей балки придется использовать те же 2 стержня диаметром 12 мм. Так как площадь сечения 2 стержней диаметром 10 мм составляет 1,57 см2.
Коэффициент армирования нашей балки согласно формулам (6.8) и (6.9) составит:
μ% = 100·0,266·145/3600 = 1,071 %
Такой процент находится в рекомендуемых пределах. Значение ξ = 0,266 меньше; ξR = 0,2911. Таким образом все необходимые и рекомендуемые условия по проектированию железобетонных элементов нами соблюдены.
Таблица 2. Площади поперечных сечений и масса арматурных стержней.
| Номинальный диаметр, мм | Площадь поперечного сечения, см2 | Масса 1 метра, теоретическая, кг |
|---|---|---|
| 6 | 0,283 | 0,222 |
| 7 | 0,385 | 0,302 |
| 8 | 0,503 | 0,395 |
| 10 | 0,785 | 0,617 |
| 12 | 1,131 | 0,888 |
| 14 | 1,54 | 1,21 |
| 16 | 2,01 | 1,58 |
| 18 | 2,64 | 2 |
| 20 | 3,14 | 2,47 |
| 22 | 3,80 | 2,98 |
| 25 | 4,91 | 3,85 |
| 28 | 6,16 | 4,83 |
| 32 | 8,04 | 6,31 |
| 36 | 10,18 | 7,99 |
| 40 | 12,58 | 9,87 |
| 45 | 15,90 | 12,48 |
Этап 8. Проверка прочности по касательным напряжениям.
Так как арматуру в верхнем слое и поперечное армирование балки (хомуты или вертикальные стержни) мы не предусматривали, то следует проверить прочность балки по касательным напряжениям, исходя из следующих условий:
где
Qmax - максимальное значение поперечной силы (определяется по эпюре поперечных сил). При нашей расчетной схеме Qmax = ql/2 = 400·4/2 = 800 кг;
Rbt - расчетное сопротивление бетона растяжению, для класса бетона B25 Rbt = 10,7 кгс/см2 (определяется по той же таблице 4);
таким образом
800 кг < 2,5·10,7·10·15,5 = 4146,25 кг
Условие прочности по касательным напряжениям нами выполняется и в этом случае расчета по сечениям, наклонным к продольной оси, не требуется. Однако это вовсе не означает, что поперечная арматура совсем не нужна. Дело в том, что мы рассчитывали балку на равномерно распределенную нагрузку, в действительности же нагрузка далеко не всегда может рассматриваться как равномерно распределенная, например, при укладке деревянных лаг с шагом 0,5-1 м по ж/б балкам, нагрузку более правильно рассматривать как несколько сосредоточенных. И даже при установке тяжеленного шкафа или, например, бильярдного стола на монолитную плиту перекрытия часть нагрузок будет явно сосредоточенными. В таких случаях и значение момента может быть несколько больше, но самое главное, возникают значительные местные напряжения. Поперечная арматура перераспределяет внутренние напряжения, а потому использование поперечной арматуры необходимо в балках, для которых все возможные нагрузки и их сочетания предусмотреть не возможно.
Пример расчета железобетонной перемычки, на действие равномерно распределенной нагрузки.
Ну и еще один пример для закрепления пройденного материала: нужно рассчитать перемычку пролетом 3 м для внутренней стены толщиной 40 см, на которую с двух сторон опираются стандартные пустотные плиты перекрытия из железобетона длиной 6 м, собственный вес плиты составляет 300-330 кг/м2. Итого суммарная расчетная нагрузка составит около 700 кг/м2, а расчетная нагрузка на погонный метр составит
700·6 = 4200 кг/м.п.
Максимальный изгибающий момент для такой балки составит
4200·32/8 = 4725 кгм.
Принимаем ширину перемычки 40 см, исходя из технологических соображений. Высоту перемычки первоначально принимаем 20 см, класс бетона и класс арматуры такие же, как и в предыдущем примере, тогда:
Аo = M/bh2oRпр = 4725/(0,4·0,182·1450000) = 0,251
По вспомогательной таблице 1 находим η = 0,853 и ξ = 0,293 (так как мы не изменяли класс бетона и арматуры то условие ξ ≤ ξR (6.1) соблюдено).
Тогда согласно формуле (6.5) требуемая площадь сечения арматуры:
Fa = M/ηh0Ra = 4725/(0,853·0,18·36000000) = 0,000854 м2 или 8,54 см2.
Для армирования перемычки можно использовать 4 стержня диаметром 18 мм. Площадь сечения арматуры составит 10,17 см2.
Коэффициент армирования нашей балки согласно формулам (6.8) и (6.9) составит:
μ% = 100·0.293·145/3600 = 1,18 %
Рекомендуемая СНиП 2.03.01-84(1996) толщина защитного слоя должна составлять не менее толщины стержня арматуры и не менее 15 мм при высоте балки до 250 мм. Это условие у нас не соблюдено, так как при а = 2 см защитный слой составит 11 мм. Чтобы соблюсти условие, необходимо поднять арматуру, из технологических соображений примем а = 3 см. Чтобы не производить полный перерасчет лучше просто увеличить высоту балки на 1 см. Таким образом высота балки составит 21 см.
Конечно, любую конструкцию не мешает проверить на прогиб, мало ли чего. И хотя железобетонные конструкции подчиняются тем же законам физики как и конструкции из любых других материалов, все же определение прогиба для железобетонной конструкции имеет свои особенности.
Для расчета балок может помочь онлайн калькулятор, которым очень легко пользоваться.